SLAM学习笔记

参考资料：

1. 《SLAM十四讲》高翔

概述

经典视觉 SLAM 框架

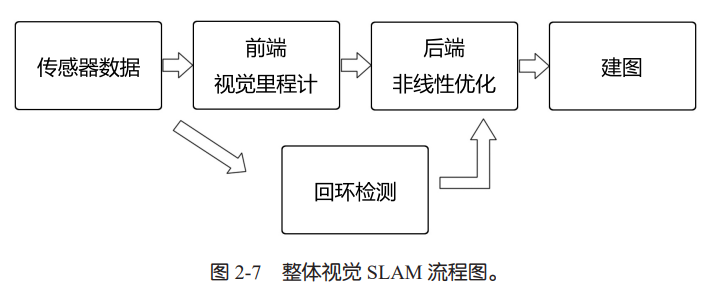
1. 传感器信息读取。在视觉 SLAM 中主要为相机图像信息的读取和预处理。如果是在机器人 中，还可能有码盘、惯性传感器等信息的读取和同步。

2. 视觉里程计（Visual Odometry，VO）。视觉里程计的任务是估算相邻图像间相机的运动，以 及局部地图的样子。VO 又称为前端（Front End）。

3. 后端优化（Optimization）。后端接受不同时刻视觉里程计测量的相机位姿，以及回环检测的 信息，对它们进行优化，得到全局一致的轨迹和地图。由于接在 VO 之后，又称为后端（Back End）。 后端优化要考虑的问题，就是如何从这些带有噪声的数据中估计整个系统的状态，以及这个状态估计的不确定性有多大——这称为最大后验概率估计（Maximum-a-Posteriori，MAP）。这里的状态既包括机器人自身的轨迹，也包含地图。

4. 回环检测（Loop Closing）。回环检测判断机器人是否到达过先前的位置。如果检测到回环， 它会把信息提供给后端进行处理。主要解决位置估计随时间漂 移的问题。

5. 建图（Mapping）。它根据估计的轨迹，建立与任务要求对应的地图。

   • 度量地图（Metric Map）

     度量地图强调精确地表示地图中物体的位置关系，通常用稀疏（Sparse）与稠密（Dense）对其 分类。当查询某个空间位置时，地图能够给出该位置是否可以通过的信息。这样的 地图可以用于各种导航算法如astar.

   • 拓扑地图（Topological Map）

     拓扑地图是一个图（Graph）， 由节点和边组成，只考虑节点间的连通性，例如 A、B 点是连通的，而不考虑如何从 A 点到达 B 点。

数学描述

• 运动方程：$u_k$ 是运动传感器的读数或者输入，$w_k$ 为该过程中加入的噪声。

  $$\boldsymbol{x}_{k}=f\left(\boldsymbol{x}_{k-1}, \boldsymbol{u}_{k}, \boldsymbol{w}_{k}\right)$$

• 观测方程：在 $xk $位置上看到某个 路标点$ y_j$，产生了一个观测数据 $z{k,j}$。$v_{k,j} $是这次观测里的噪声

  $$\boldsymbol{z}_{k, j}=h\left(\boldsymbol{y}_{j}, \boldsymbol{x}_{k}, \boldsymbol{v}_{k, j}\right)$$

• 这两个方程描述了最基本的 SLAM 问题：当知道 运动测量的读数$ u$，以及传感器的读数$ z$ 时，如何求解定位问题（估计$ x$）和建图问题（估计$ y$）？ 这时，我们就把 SLAM 问题建模成了一个状态估计问题：如何通过带有噪声的测量数据，估计内部 的、隐藏着的状态变量？

三维刚体运动

• 旋转矩阵：矩阵由两组基之间的内积组成，刻画了旋转 前后同一个向量的坐标变换关系。同时，该矩阵各分量是两个坐标系基的内 积，由于基向量的长度为 1，所以实际上是各基向量的夹角之余弦。所以这个矩阵也叫方向余弦矩阵（Direction Cosine matrix）。

  $$\left[\begin{array}{l} a_{1} \\ a_{2} \\ a_{3} \end{array}\right]=\left[\begin{array}{lll} \boldsymbol{e}_{1}^{\mathrm{T}} \boldsymbol{e}_{1}^{\prime} & \boldsymbol{e}_{1}^{\mathrm{T}} \boldsymbol{e}_{2}^{\prime} & \boldsymbol{e}_{1}^{\mathrm{T}} \boldsymbol{e}_{3}^{\prime} \\ \boldsymbol{e}_{2}^{\mathrm{T}} \boldsymbol{e}_{1}^{\prime} & \boldsymbol{e}_{2}^{\mathrm{T}} e_{2}^{\prime} & \boldsymbol{e}_{2}^{\mathrm{T}} \boldsymbol{e}_{3}^{\prime} \\ \boldsymbol{e}_{3}^{\mathrm{T}} \boldsymbol{e}_{1}^{\prime} & \boldsymbol{e}_{3}^{\mathrm{T}} \boldsymbol{e}_{2}^{\prime} & \boldsymbol{e}_{3}^{\mathrm{T}} \boldsymbol{e}_{3}^{\prime} \end{array}\right]\left[\begin{array}{l} a_{1}^{\prime} \\ a_{2}^{\prime} \\ a_{3}^{\prime} \end{array}\right] \triangleq \boldsymbol{R} \boldsymbol{a}^{\prime}$$
  • 旋转矩阵是一个行列式为 1 的正交矩阵

• SO(n) 特殊正交群（Special Orthogonal Group）：n 维旋转矩阵的集合

  $$\operatorname{SO}(n)=\left\{\boldsymbol{R} \in \mathbb{R}^{n \times n} \mid \boldsymbol{R} \boldsymbol{R}^{\mathrm{T}}=\boldsymbol{I}, \operatorname{det}(\boldsymbol{R})=1\right\}$$

• 齐次坐标和变换矩阵：可以把旋转和平移写在一个矩阵里面，使得整个关系变成线性关系

  $$\left[\begin{array}{l} \boldsymbol{a}^{\prime} \\ 1 \end{array}\right]=\left[\begin{array}{ll} \boldsymbol{R} & \boldsymbol{t} \\ \mathbf{0}^{\mathrm{T}} & 1 \end{array}\right]\left[\begin{array}{l} \boldsymbol{a} \\ 1 \end{array}\right] \triangleq \boldsymbol{T}\left[\begin{array}{l} \boldsymbol{a} \\ 1 \end{array}\right]$$

• 特殊欧氏群（Special Euclidean Group）

  $$\mathrm{SE}(3)=\left\{\boldsymbol{T}=\left[\begin{array}{cc} \boldsymbol{R} & \boldsymbol{t} \\ \mathbf{0}^{\mathrm{T}} & 1 \end{array}\right] \in \mathbb{R}^{4 \times 4} \mid \boldsymbol{R} \in \mathrm{SO}(3), \boldsymbol{t} \in \mathbb{R}^{3}\right\}$$
  • T的逆变换 $$\boldsymbol{T}^{-1}=\left[\begin{array}{cc} \boldsymbol{R}^{\mathrm{T}} & -\boldsymbol{R}^{\mathrm{T}} \boldsymbol{t} \\ \mathbf{0}^{\mathrm{T}} & 1 \end{array}\right]$$

• 罗德里格斯公式：旋转向量到旋转矩阵的转换过程，符号 ∧ 是向量到反对称的转换符（对于外积引入的符号，记为反对称符号，把外积a×b写成了矩阵与向量的乘法，变成线性运算）

  $$\boldsymbol{R}=\cos \theta \boldsymbol{I}+(1-\cos \theta) \boldsymbol{n} \boldsymbol{n}^{\mathrm{T}}+\sin \theta \boldsymbol{n}^{\wedge}$$

• 已知R求n和theta：转轴 n 是矩阵 R 特征值 1 对应的特征向量。

  $$\begin{array}{c} \theta = \arccos \left(\frac{\operatorname{tr}(\boldsymbol{R})-1}{2}\right)\\ \boldsymbol{R} \boldsymbol{n} = \boldsymbol{n} \end{array}$$

• 欧拉角

  • 步骤
    1. 绕物体的 Z 轴旋转，得到偏航角 yaw；
    2. 绕旋转之后的 Y 轴旋转，得到俯仰角 pitch；
    3. 绕旋转之后的 X 轴旋转，得到滚转角 roll。
  • 万向锁问题（Gimbal Lock）：在俯仰角为 ±90◦ 时，第 一次旋转与第三次旋转将使用同一个轴，使得系统丢失了一个自由度（由 3 次旋转变成了 2 次旋转）。欧拉角不适于插值和迭代，往往只用于人机交互中。我们也很少在 SLAM 程序中直接使用欧拉角表达姿态，同样不会在滤波或优化中使用欧拉角表达旋转（因为它具有奇异性）。

• 四元数

  • 旋转矩阵用 9 个量描述 3 自由度的旋转，具有冗余性；欧拉角和旋转向量是紧凑的，但具有奇 异性。事实上，我们找不到不带奇异性的三维向量描述方式

  • 在表达三维空间旋转时， 也有一种类似于复数的代数：四元数（Quaternion）。四元数是 Hamilton 找到的一种扩展的复数。它 既是紧凑的，也没有奇异性。如果说缺点，四元数不够直观，其运算稍复杂些。

  • 一个四元数 q 拥有一个实部和三个虚部。

    $$q = q_0 + q_1i + q_2j + q_3k$$
    • 乘法是把 qa 的每一项与 qb 的每项相乘，最后相加
    • 四元数乘法通常是不可交换的
    • 两个四元数乘积的模即为模的乘积
    • 四元数的共轭是把虚部取成相反数
    • 四元数共轭与其本身相乘，会得到一个实四元数，其实部为模长的平方
    • 逆：$q^{-1}=q^*/\left | q \right |^2 $

  • 用四元数表示旋转,相当于把四元数的 3 个虚部与空间中的 3 个轴相对应。计算$p’=qpq^{-1}$.这里的乘法均为四元数乘法，结果也是四元数。最后把 p ′ 的虚部取出，即得旋转之后点的坐标。并且，计算结果的实部为 0，故为纯虚四元数。

  • 四元数到其他旋转表示的转换

    pass

  • 在实际编程中，程序库 通常会为我们准备好各种形式之间的转换。无论是四元数、旋转矩阵还是轴角，它们都可以用来描 述同一个旋转。

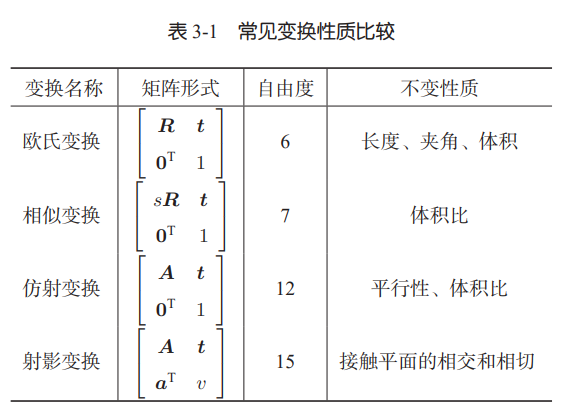
• 相似、仿射、射影变换

  

李群、李代数

相机与图像

相机模型

• 单目

  • 可参考北邮《计算机视觉》笔记

• 双目

  • 可参考北邮《计算机视觉》笔记

• RGB-D

  • 原理

    • 通过红外结构光（Structured Light）
    • 通过飞行时间法（Time-of-flight，ToF）

  • RGB-D 相机能够实时地测量每个像素点的距离。但是，由于这种发射 − 接收的测量方式，其使 用范围比较受限。用红外光进行深度值测量的 RGB-D 相机，容易受到日光或其他传感器发射的红外光干扰，因此不能在室外使用。在没有调制的情况下，同时使用多个 RGB-D 相机时也会相互干 扰。对于透射材质的物体，因为接收不到反射光，所以无法测量这些点的位置。此外，RGB-D 相机 在成本、功耗方面，都有一些劣势。

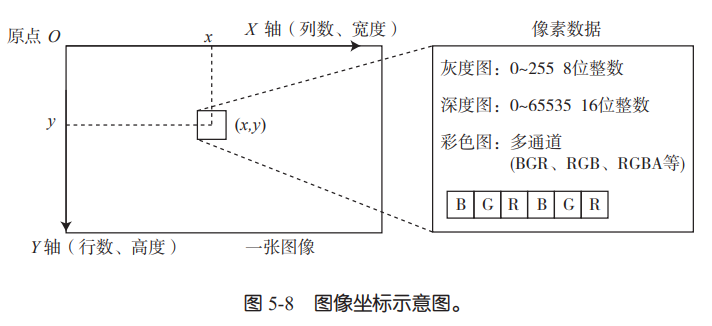
图像模型

非线性优化

• 理解最小二乘法的含义和处理方式。
• 理解高斯牛顿法（Gauss-Newton）、列文伯格—马夸尔特方法（LevenburgMarquadt）等下降策略。
• 学习 Ceres 库和 g2o 库的基本使用方法。

视觉里程计

应用