《人工智能控制》笔记

本文最后更新于：2022年5月21日 14:27

2022年春《人工智能控制》课程笔记

2022年4月20日

归纳：hjy，lcy

校对：swh

知识表示

知识

具有相对正确性、不正确性、可表示性、可利用性
知识表示：将人类知识形式化或者模型化。知识表示是对知识的一种描述，或者说是一组约定，一种计算机可以接受的用于描述知识的数据结构

一阶谓词逻辑表示法

命题：非真即假的陈述句（一个命题在不同条件下真值可能改变）
个体：可以是常量、变量、函数、谓词
谓词公式连接词：否定 $\neg$ 、析取 $\vee$ 、合取 $\wedge$ 、蕴含 $\rightarrow$ 、等价 $\leftrightarrow$
量词：全称量词 $\forall$ 、存在量词 $\exists$ ，（出现顺序将影响命题含义）
谓词公式：原子谓词公式的有限步套娃缝合
连接词和量词的优先级是如上出现的顺序由高到低
量词辖域：位于量词后面的单个谓词或者用括孤括起来的谓词公式
约束变元与自由变元：辖域内，与量词中同名的变元称为约束变元，不同名的变元称为自由变元
谓词公式在个体域上的解释：个体域中的实体对谓词演算表达式的每个常量、变量谓词和函数符号的指派，对于每一个解释，谓词公式都可以求出一个真值
永真、永假、可满足、不可满足
- 如果谓词公式P对个体域D上的任何一个解释都取得真值T,则称P在D上是永真的；如果P在每个非空个体域上均永真，则称P永真
- 如果谓词公式P对个体域D上的任何一个解释都取得真值F,则称P在D上是永假的；如果P在每个非空个体域上均永假，则称P永假。
- 对于谓词公式P，如果至少存在一个解释使得P在此解释下的真值为T，则称P是可满足的，否则，不存在任何一个解释，则称P是不可满足的。
常用推导：
- 德摩根
- 蕴含转换：$P \rightarrow Q \Rightarrow \neg P \vee Q$
- 反证法：把结论取反，带入已知条件，推导出F
特点
- 优点：自然、精确、严密、容易实现
- 局限：不能表示不确定的知识、组合爆炸、效率低

产生式表示法

产生式作用：通常用于表示事实、规则以及它们的不确定性度量，适合于表示事实性知识和规则性知识。
表示
- 确定性规则知识：if P then Q
- 不确定性规则知识：if P then Q (alpha)
- 确定性事实性知识：(obj, key, value) (relation, obj1, obj2)
- 不确定性事实性知识：(obj, key, value, alpha) (relation, obj1, obj2, alpha)
产生式与谓词逻辑中的蕴含式的区别
- 除逻辑蕴含外，产生式还包括各种操作、规则、变换、算子、函数等。例如，如果炉温超过上限，则立即关闭风门 是一个产生式（关联），但不是蕴含式（因果）。
- 蕴含式只能表示精确知识，而产生式不仅可以表示精确的知识，还可以表示不精确知识。蕴含式的匹配总要求是精确的。产生式匹配可以是精确的，也可以是不精确的，只要按某种算法求出的相似度落在预先指定范围内就认为是可匹配的。
特点
- 优点：自然、模块、有效、清晰
- 局限：效率不高、不能表达结构性知识
- 适用：知识不存在结构关系，知识是经验性的、不确定的，没有统一理论的、求解过程可被表示为一系列相对独立的操作，且每个操作可被表示为产生式规则

框架表示法

框架：一种描述所论对象（一个事物、事件或概念)，属性的数据结构。
一个框架由若干个槽组成，每一个槽又可分为侧面。
一个槽用于描述所论对象某一方面的属性。一个侧面用于描述相应属性的一个方面。
槽和侧面所具有的属性值分别被称为槽值和侧面值。
特点：结构性、继承性、自然性

确定性推理方法

推理

演绎推理：一般到个别（三段论）
归纳推理：个别到一般（完全归纳、不完全归纳）
默认推理
确定性推理：知识证据确定、推出结论确定
不确定性推理：知识证据不确定、推出结论不确定（似然推理：概率论、模糊推理：模糊逻辑）
单调推理、非单调推理
启发式推理、非启发式推理
推理方向
- 正向推理：事实驱动推理，已知事实到结论，简单易实现，目的性不强，效率低
- 逆向推理：目标驱动推理，以某个假设目标作为出发点，不必使用和目标无关的知识，目的性强，有利于向用户提供解释，但是起始目标的选择具有盲目性，比较复杂
- 混合推理：先正后反，先反后正
- 双向推理：同时进行到中间的结论
冲突消解策略：排序，按照针对性、事实新鲜性、匹配度、条件个数划分优先级

自然演绎推理

自然演绎推理：从一组已知为真的事实出发，运用经典逻辑的推理规则推出结论的过程。（P规则、T规则、假言推理、拒取式推理）（其实直接记住P→Q的真值表就行，不过考试只考假言推理）
- 假言：$P \rightarrow Q , P\Rightarrow Q $
- 拒取：$P \rightarrow Q , \neg Q \Rightarrow \neg P $
常见错误
- 否定前件： $P \rightarrow Q , \neg P\Rightarrow \neg Q (\cross)$
- 肯定后件：$P \rightarrow Q , Q \Rightarrow P (\cross)$
特点
- 优点：表达定理证明过程自然，易理解。拥有丰富的推理规则，推理过程灵活。便于嵌入领域启发式知识。
- 缺点：易产生组合爆炸，得到的中间结论一般呈指数形式递增。

题目：谓词公式转化子句集

定义：原子谓词公式（不可分解的命题）、文字（原子及其否定）、子句（文字的析取式）（离散中的主析取范式）、空子句NIL、子句集合
▲谓词公式转化子句集解题步骤
1. 使用公式消去 $\rightarrow $ 和 $\leftrightarrow $ 符号
2. 否定后移，把 $\neg$ 移动到紧靠谓词的位置
3. 变量标准化，在不同辖域的时候用了同一个自变量符号需要换一个
4. 消除 $\exists$ ，用 $x$ 的函数代替（用出现在 $\exists$ 左边的所有的 $\forall$ 中的变量代替，因此可能是多元函数，如果没有，就写为常量）
5. 化为前束型 (前缀){母式} ，前缀是全称量词串，母式是不含量词的谓词公式
6. 化为 Skolem 标准型 $\left(\forall x{1}\right)\left(\forall x{2}\right) \cdots\left(\forall x_{n}\right) M$ ，这里要用的又是合取范式
7. 省略 $\forall$
8. 省略 $\wedge$，也就是写成合取范式每个项的集合形式
9. 子句变量标准化，也就是每个子句使用不同的自变量

例题

将下列谓词公式化为子句集
$(\forall x)\{[\neg P(x) \vee \neg Q(x)] \rightarrow(\exists y)[S(x, y) \wedge Q(x)]\} \wedge(\forall x)[P(x) \vee B(x)]$
解答
$(\forall x)\{\underline{[\neg P(x) \vee \neg Q(x)] \rightarrow(\exists y)[S(x, y) \wedge Q(x)]}\} \wedge(\forall x)[P(x) \vee B(x)] \\ (\forall x)\{\underline{\neg[\neg P(x) \vee \neg Q(x)]} \vee(\exists y)[S(x, y) \wedge Q(x)]\} \wedge(\forall x)[P(x) \vee B(x)] \\ (\forall x)\{[P(x) \wedge Q(x)] \vee(\exists y)[S(x, y) \wedge Q(x)]\} \wedge\underline{(\forall x)}[P(\underline{x}) \vee B(\underline{x})] \\ (\forall x)\{[P(x) \wedge Q(x)] \vee\underline{(\exists y)}[S(x, \underline{y}) \wedge Q(x)]\} \wedge(\forall w)[P(w) \vee B(w)] \\ \underline{(\forall x)}\{[P(x) \wedge Q(x)] \vee[S(x, f(x)) \wedge Q(x)]\} \wedge \underline{(\forall w)}[P(w) \vee B(w)] \\(\forall x)(\forall w)\{\{[P(x) \wedge \underline{Q(x)}] \vee[S(x, f(x)) \wedge \underline{Q(x)}]\} \wedge[P(w) \vee B(w)]\} \\\underline{(\forall x)(\forall w)}\{Q(x) \wedge[P(x) \vee S(x, f(x))] \wedge[P(w) \vee B(w)]\} \\Q(x) \underline{\wedge}[P(x) \vee S(x, f(x))] \underline{\wedge}[P(w) \vee B(w)] \\\{Q(x), P(x) \vee S(\underline{x}, f(\underline{x})), P(w) \vee B(w)\} \\子句集 = \{Q(x), P(y) \vee S(y, f(y)), P(w) \vee B(w)\}$
例题与解答

鲁宾逊归结原理

谓词公式不可满足的充要条件：其子句集不可满足
子句集中子句之间是合取关系，只要有一个子句不可满足，则子句集就不可满足
鲁宾逊归结原理的基本思想：检查子句集中是否包含空子句，若包含，则子句集不可满足。若不包含，在子句集中选择合适的子句进行归结，一旦归结出空子句，就说明子句集是不可满足的
归结：设 $C{1}$ 与 $C{2}$ 是子句集中的任意两个子句，如果 $C{1}$ 中的文字 $L{1}$ 与 $C{2}$ 中的文字 $L{2}$ 互补, 那么从 $C{1}$ 和 $C{2}$ 中分别消去 $L{1}$ 和 $L{2}$ ，并将二个子句中余下的部分析取，构成新子句 $C_{12}$ 。
亲本子句为真，则归结的式子也为真
新推导的子句代替被推导的子句后加入原子句集，则新子句集的不可满足性可以推出原子句集的不可满足性
新推导的子句加入原子句集，则新子句集的不可满足性和原子句集的不可满足性等价
含有变量的子句的归结（归结前，两个子句集的同一个参数名仍需改为不一样的）
$C_{1}=P(x) \vee Q(a), C_{2}=\neg P(b) \vee R(x) \\令 C_{2}=\neg P(b) \vee R(y), \sigma=\{b / x\} \\ \rightarrow C_{1} \sigma=P(b) \vee Q(a), C_{2} \sigma=\neg P(b) \vee R(y) \\ \rightarrow C_{12}=Q(a) \vee R(y)$
对于谓词逻辑，归结式是其亲本子句的逻辑结论
对于一阶谓词逻辑，即若子句集是不可满足的，则必存在一个从该子句集到空子句的归结演绎；若从子句集存在一个到空子句的演绎，则该子句集是不可满足的。
如果没有归结出空子句，则既不能子句集说不可满足，也不能说子句集是可满足的

题目：归结反演

归结反演：应用归结原理证明定理的过程
▲归结反演证明题步骤
1. 将已知前提表示为谓词公式 $F$。
2. 将待证明的结论表示为谓词公式 $Q$ ，并否定得到 $\neg Q$ 。
3. 把谓词公式集 ${F, \neg Q}$ 化为子句集 $S$ 。
4. 应用归结原理对子句集 $S$ 中的子句进行归结，并把每次归结得到的归结式都并入到 $S$ 中。反复进行，若出现了空子句，则停止归结，此时就证明了 $Q$ 为真。

例题

已知：任何人的兄弟不是女性；任何人的姐妹必是女性。
事实：Mary 是 Bill 的姐妹。
求证：Mary 不是 Tom 的兄弟。

解答

定义谓词

$brother(x,y)$ $x$ 是 $y$ 的兄弟
$sister(x,y)$ $x$ 是 $y$ 的姐妹
$woman(x)$ $x$ 是女性

使用谓词公式表示出已知规则和结论的否定
$(\forall x)(\forall y)( brother (x, y) \rightarrow \neg woman (x)) \\(\forall x)(\forall y)({sister}(x, y) \rightarrow woman (x)) \\ sister (Mary, Bill) \\ brother(Mary, Tom)$
公式转换为子句集
$\begin{array}{l} (1): \neg brother (x, y) \vee \neg woman (x) \\(2): \neg sister(x, y) \vee woman (x) \\(3): sister( Mary, Bill) \\(4): brother(Mary , Tom ) \end{array}$
选择合适的步骤归结子句集到空子句（先归结1和2不能得到空子句）
$\begin{array}{l} (5):Lwoman ( Mary ) && (1)(3)\\ (6):\neg brother ( Mary, y) &&(4)(5)\\ (7):NIL && (2)(6) \end{array}$

▲归结反演应用题步骤
1. 将已知前提表示为谓词公式 $F$。
2. 将待求解的结论表示为 $Q$ ，否定得到$\neg Q$ ，与 $ANSWER$ 构成析取式 $\neg Q \vee ANSWER$。
3. 把谓词公式集 ${ F, \neg Q \vee ANSWER }$ 化为子句集 $S$ 。
4. 应用归结原理对 $S$ 中子句进行归结，并把每次归结得到的归结式都并入到 $S$ 中。反复进行，若得到归结式 $ANSWER$ ，则答案就在 $ANSWER$ 中。

例题

已知：老王是小李的老师。小李与小张是同班同学。如果 $x$ 与 $y$ 是同班同学，则 $x$ 的老师也是 $y$ 的老师。

求解：小张的老师是谁。

解答

定义谓词

$T(x,y)$ $x$ 是 $y$ 的老师
$C(x,y)$ $x$ 与 $y$ 是同班同学

使用谓词公式表示出已知规则，以及待求解的结论与答案的析取式
$T(Wang,Li ) \\ C( Li,Zhang ) \\ (\forall x)(\forall y)(\forall z)(C(x, y) \wedge T(z, x) \rightarrow T(z, y)) \\ \neg(\exists x) T(x, Zhang ) \vee ANSWER(x)$
公式转换为子句集
$\begin{array}{l} (1): T(Wang, Li) \\ (2):C( Li,Zhang ) \\ (3):\neg C(x, y) \vee \neg T(z, x) \vee T(z, y) \\ (4):\neg T(u , Zhang) \vee ANSWER(u) \end{array}$
应用归结原理进行归结
$\begin{array}{l} (5): \neg C( Li, y) \vee T (Wang, y) &&(1)(3) \\ (6): \neg C( Li, Zhang ) \vee ANSWER (Wang) &&(4)(5) \\ (7): ANSWER(Wang)&&(2)(6) \end{array}$

不确定性推理方法

不确定推理

不确定性推理：从不确定性的初始证据出发，通过运用不确定性的知识，最终推出具有一定程度的不确定性但却是合理或者近乎合理的结论的思维过程。
不确定性
- 知识的不确定性（静态强度）
- 证据的不确定性（动态强度，初始证据和推导出的结论作为证据）

可信度方法

可信度：根据经验对一个事物或现象为真的相信程度。可信度带有较大的主观性和经验性，其准确性难以把握。
C-F模型：基于可信度表示的不确定性推理的基本方法
▲不确定性的表示
- 知识的不确定性 CF(H,E)
  - IF E THEN H(CF(H,E))
  - CF：可信度因子，CF(H,E)反映前提条件E和结论H的联系强度，$CF \in [-1,1]$
  - 若由于相应证据的出现增加结论H为真的可信度，则 $CF(H,E) > 0 $ ,证据的出现越是支持H为真，就使 $CF(H,E) $ 的值越大。
  - 反之， $CF(H,E) < 0 $ ，证据的出现越是支持H为假， $CF(H,E) $ 的值就越小。
  - 如果证据E的出现和结论H无关，则 $CF(H,E) = 0$
- 证据的不确定性 CF(E)
  - 证据E的可信度取值范围 $CF \in [-1,1]$
  - 对于初始证据，若所有观察S能肯定它为真，则 $CF(E) = 1$
  - 若肯定它为假，则 $CF(E) = -1$
  - 若以某种程度为真，则 $0 < CF(E) < 1$，若以某种程度为假，则 $-1 < CF(E) < 0$
  - 若未获得任何相关的观察，则 $CF(E) = 0$
▲不确定性的计算
- 组合证据的不确定算法(最大最小法)
  - 合取$\and$：$CF(E) = \min { CF(E_1),CF(E_1),…,CF(E_n)}$
  - 析取$\or$：$CF(E) = \max { CF(E_1),CF(E_1),…,CF(E_n)}$
- 不确定性的传递算法
  - $CF(H)=CF(H, E) \cdot \max {0, CF(E)}$
- 结论不确定性的合成算法
  - 已知
    IF $E_1$ THEN H (CF(H,$E_1$))
    IF $E_2$ THEN H (CF(H,$E_2$))
  - 先对每一条知识求出 $CF(H)$
    $CF_1(H)=CF(H, E_1) \cdot \max {0, CF(E_1)}$
    $CF_2(H)=CF(H, E_2) \cdot \max {0, CF(E_2)}$
  - 再求出 $E1$ 和 $E_2$ 综合影响形成的可信度 $CF{1,2}(H)$
    $C F_{1,2}(H)=\left\{\begin{array}{ccc} C F_{1}(H)+C F_{2}(H)-C F_{1}(H) C F_{2}(H) & \text { 若 } C F_{1}(H) \geqslant 0, C F_{2}(H) \geqslant 0 \\ C F_{1}(H)+C F_{2}(H)+C F_{1}(H) C F_{2}(H) & \text { 若 } C F_{1}(H)<0, C F_{2}(H)<0 \\ \frac{C F_{1}(H)+C F_{2}(H)}{1-\min \left\{\left|C F_{1}(H)\right|,\left|C F_{2}(H)\right|\right\}} & \text { 若 } C F_{1}(H) \text { 与 } C F_{2}(H) \text { 异号 } \end{array}\right.$

例题

IF $E_1$ THEN H (0.8)
IF $E_2$ THEN H (0.6)
IF $E_3$ THEN H (-0.5)
IF $E_4$ AND ( $E_5$ OR $E_6$ ) THEN $E_1$ (0.7)
IF $E_7$ AND $E_8$ THEN $E_3$ (0.9)

$CF(E_2)=0.8,CF(E_4)=0.5,CF(E_5)=0.6$
$CF(E_6)=0.7,CF(E_7)=0.6,CF(E_8)=0.9$

求 $CF(H)$

解答

求组合证据的不确定性
$\begin{array}{l} CF(E_4 \enspace AND \enspace( E_5 \enspace OR \enspace E_6)) = \min \{0.5, \max \{ 0.6, 0.7\}\} = 0.5 \\ CF(E_7 \enspace AND \enspace E_8) = \min \{0.6, 0.9\} = 0.6 \\ \end{array}$
求非最终结果（临时结论）的传递不确定性
$\begin{array}{l} CF(E_1) = 0.7 \cdot \max \{0, CF(E_4 \enspace AND \enspace( E_5 \enspace OR \enspace E_6)\} = 0.7 \cdot 0.5 = 0.35 \\ CF(E_3) = 0.9 \cdot \max \{0, CF(E_7 \enspace AND \enspace E_8)\} = 0.9 \cdot 0.6 = 0.54 \\ \end{array}$
求最终结果的分结论不确定性
$\begin{array}{l} CF_1(H) = 0.8 \cdot \max \{0, CF(E_1)\} = 0.28 \\ CF_2(H) = 0.6 \cdot \max \{0, CF(E_2)\} = 0.48 \\ CF_3(H) = -0.5 \cdot \max \{0, CF(E_3)\} = -0.27 \end{array}$
求分结论合成后的不确定性
$\begin{aligned} C F_{1,2}(H) &=C F_{1}(H)+C F_{2}(H)-C F_{1}(H) \times C F_{2}(H) \\ &=0.28+0.48-0.28 \times 0.48=0.63 \\ C F_{1,2,3}(H) &=\frac{C F_{1,2}(H)+C F_{3}(H)}{1-\min \left\{\left|C F_{1,2}(H)\right|,\left|C F_{3}(H)\right|\right\}} \\ &=\frac{0.63-0.27}{1-\min \{0.63,0.27\}}=\frac{0.36}{0.73}=0.49 \end{aligned}$

证据理论

样本空间：设D是变量x所有可能取值的集合，且D中的元素是互斥的，在任一时刻x都取且只能取D中的某一个元素为值，则称D为x的样本空间。
概率分配函数：函数 $ M: 2^{D} \rightarrow[0,1]$ ，且满足如下划分条件

则 $M: 2^{D}$ 上的基本概率分配函数, $M(A): A$ 的基本概率数
- $M(A)$ 为命题A的精确信任度
- 概率分配函数和概率是不同的：对于概率分配函数，D的幂集所有元素的函数之和为1；对于概率，D所有元素的函数之和为1）
概率分配函数的正交和计算（证据的组合）
- $K$ 称为归一化因子，反映证据的冲突程度，如果 $K \neq 0$，则正交和也是一个概率分配函数；如果 $K = 0$，则不存在正交和，得到 $M_1 $ 和 $ M_2$ 矛盾
- 计算 $\sum_{x \cap y = A} M_1(x)M_2(y)$ 时，注意 $x$ 和 $y$ 是可以相等的
信任函数：函数 $Bel: 2^{D} \rightarrow[0,1]$ ，且满足如下划分条件
- $Bel(A)$ 为命题A的真的总的信任度，是信任度下限
似然函数：函数 $Pl: 2^{D} \rightarrow[0,1]$ ，且满足如下转换条件
- $Pl(A)$ 为命题A的非假的信任度，为信任度上限
▲基于证据理论的不确定性推理的步骤
1. 建立问题的样本空间D
2. 分别计算两个证据的概率分配函数
3. 计算组合概率分配函数
4. 计算信任函数（下限）
5. 计算似然函数（上限）
6. 得出结论

例题

设有规则

IF 流鼻涕 THEN 感冒但非过敏性鼻炎(0.9) OR 过敏性鼻炎但非感冒(0.1)
IF 眼发炎 THEN 感冒但非过敏性鼻炎(0.8) OR 过敏性鼻炎但非感冒(0.05)

又有事实

小王流鼻涕(0.9)
小王眼发炎(0.4)

求解小王患的什么病

解答

建立假设结果（患病情况）的样本空间

$D = \{A,B\} \\ M = \{\{A\},\{B\},\{A,B\},\varnothing\} \\ A: 感冒 \\ B：过敏性鼻炎$

分别计算两个证据的基本概率分配函数

小王流鼻涕(0.9)时，计算 $M_1$

$\begin{array}{l} M_1(\varnothing) = 0 \\ M_1(A) = 0.9\times 0.9 = 0.81 \\ M_1(B) = 0.9\times 0.1 = 0.09 \\ M_1(AB) = 1 - M_1(A) - M_1(B) = 0.1 \\ M_1(\{A\},\{B\},\{A,B\},\{\varnothing\}) = (0.81,0.09,0.1,0) \end{array}$

小王眼发炎(0.4)时，计算 $M_2$

$\begin{array}{l} M_2(\varnothing) = 0 \\ M_2(A) = 0.4\times 0.8 = 0.32 \\ M_2(B) = 0.4\times 0.05 = 0.02 \\ M_2(AB) = 1 - M_1(A) - M_1(B) = 0.66 \\ M_2(\{A\},\{B\},\{A,B\},\{\varnothing\}) = (0.32,0.02,0.66,0) \end{array}$

计算组合概率分配函数

先计算 $K$

$\begin{array}{l} K\\ = 1 - \sum_{x \cap y = \varnothing}M_1(x)M_2(y)\\ =1 - [M_1(\{A\})M_2(\{B\}) + M_1(\{B\})M_2(\{A\})] \\ = 1 - [0.81\times0.02 + 0.09\times0.32] = 0.955 \end{array}$

流鼻涕的组合概率分配函数 0.87

$\begin{array}{l} M(A) \\ = K^{-1}\sum_{x \cap y = A}M_1(x)M_2(y) \\ = K^{-1}[M_1(\{A\})M_2(\{A\}) + M_1(\{A\})M_2(\{A,B\}) + M_1(\{A,B\})M_2(\{A\})] \\ = \frac{1}{0.955} \times 0.8258 = 0.87 \end{array}$

眼发炎的组合概率分配函数 0.066

$\begin{array}{l} M(B) \\ = K^{-1}\sum_{x \cap y = B}M_1(x)M_2(y) \\ = K^{-1}[M_1(\{B\})M_2(\{B\}) + M_1(\{B\})M_2(\{A,B\}) + M_1(\{A,B\})M_2(\{B\})] \\ = \frac{1}{0.955} \times 0.0632 = 0.066 \end{array}$

计算信任函数（下限） 0.87 和 0.066

$Bel(A) = \sum_{B \subseteq A} M(B) , \forall A \subseteq D$ $\begin{array}{l} Bel(\varnothing) = 0 \\ Bel(A) = M(\varnothing) + M(A) = 0.87 \\ Bel(B) = M(\varnothing) + M(B) = 0.066 \\ Bel(AB) = M(\varnothing) + M(A) + M(B) = 0.064 \end{array}$

计算似然函数（上限） 0.934 和 0.13

$Pl(A)=1-Bel(\neg A), \forall A \subseteq D$ $\begin{array}{l} Pl(A) \\ = 1 - Bel(\neg A) \\ = 1 - [Bel(B) + Bel(\varnothing)] \\ = 1- [0.066 + 0] = 0.934 \\ \\ Pl(B) \\ = 1 - Bel(\neg B) \\ = 1 - [Bel(A) + Bel(\varnothing)] \\ = 1- [0.87 + 0] = 0.13 \end{array}$

由信任函数值、似然函数值得出结论
感冒为真的信任度0.87 ，非假的信任度0.934
过敏性鼻炎为真的信任度0.066，非假的信任度0.13
小王大概率为感冒

模糊推理方法

论域：所讨论的全体对象，用U等表示。
元素：论域中的每个对象，常用a,b,c,x,y,z表示。
集合：论域中具有某种相同属性的确定的、可以彼此区别的元
素的全体，常用A,B等表示。
元素a和集合A的关系：a属于A或a不属于A
模糊逻辑给集合中每一个元素赋予一个介于0和1之间的实数，描述其属于一个集合的强度，该实数称为元素属于一个集合的隶属度。集合中所有元素的隶属度全体构成集合的隶属函数
表示方法：Zadeh、序偶、向量
$A=\left\{\mu_{A}\left(x_{1}\right) / x_{1}, \mu_{A}\left(x_{2}\right) / x_{2}, \cdots, \mu_{A}\left(x_{n}\right) / x_{n}\right\} \\ A=\int_{x \in U} \mu_{A}(x) / x$
隶属函数
模糊集合运算

$\begin{array}{l} \mu_{A \cap B}(x)=\min \left\{\mu_{A}(x), \mu_{B}(x)\right\}=\mu_{A}(x) \wedge \mu_{B}(x) \\ \mu_{A \cup B}(x)=\max \left\{\mu_{A}(x), \mu_{B}(x)\right\}=\mu_{A}(x) \vee \mu_{B}(x) \\ \mu_{\overline{A} }(x)=1-\mu_{A}(x) \\ \\ \mu_{A B}(x)=\mu_{A}(x) \mu_{B}(x) \\ \mu_{A+B}(x)=\mu_{A}(x)+\mu_{B}(x)-\mu_{A}(x) \mu_{B}(x) \\ \mu_{A \oplus B}(x)=\min \left\{1, \mu_{A}(x)+\mu_{B}(x)\right\}=1 \wedge\left[\mu_{A}(x)+\mu_{B}(x)\right] \\ \mu_{A \otimes B}(x)=\max \left\{0, \mu_{A}(x)+\mu_{B}(x)-1\right\}=0 \vee\left[\mu_{A}(x)+\mu_{B}(x)-1\right] \end{array}$

模糊关系运算：模糊关系使用叉积表示（用$\wedge$，不是数字相乘）

$R: A \times B \rightarrow[0,1] \\ R = \mu_{A \times B}(a, b)=\mu_{A}^{T} \circ \mu_{B}$

模糊推理

$A \circ B=\vee_{k=1}^{l}\left(a_{i k} \wedge b_{k j}\right)\\ B'=A' \circ R$

模糊决策
- 最大隶属度法（maxarg）
- 加权平均法
- 中位数法
  直接相等时 $ sum(list[:j+1]) == sum(list[j+1:])$ 取 $u=j$
  否则找到最后一个 $ sum(list[:j+1]) < sum(list[j+1:])$ ，令 $u=j+sum(list[j+1:])/sum(list)$

题目：模糊推理应用

▲求解模糊控制的度量步骤
1. 模糊关系运算，求模糊关系
2. 模糊推理，求输出
3. 使用合适决策方法，求决策度量

例题

已知：如果温度低，则将风门开大。

设温度和风门开度的论域为 ${1,2,3,4,5}$。
温度低=1/1+0.6/2+0.3/3+0.0/4+0/5
风门大=0/1+0.0/2+0.3/3+0.6/4+1/5

已知事实：温度较低=0.8/1+1/2+0.6/3+0.3/4+0/5
试用模糊推理确定风门开度。

解答
$R=\left[\begin{array}{l} 1.0 \\ 0.6 \\ 0.3 \\ 0.0 \\ 0.0 \end{array}\right] \circ\left[\begin{array}{lllll} 0.0 & 0.0 & 0.3 & 0.6 & 1.0 \end{array}\right]=\left[\begin{array}{ccccc} 0.0 & 0.0 & 0.3 & 0.6 & 1.0 \\ 0.0 & 0.0 & 0.3 & 0.6 & 0.6 \\ 0.0 & 0.0 & 0.3 & 0.3 & 0.3 \\ 0.0 & 0.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 0.0 & 0.0 \end{array}\right] \\ \\ B^{\prime}=A^{\prime} \circ R=\left[\begin{array}{l} 0.8 \\ 1.0 \\ 0.6 \\ 0.3 \\ 0.0 \end{array}\right] \circ\left[\begin{array}{lllll} 0.0 & 0.0 & 0.3 & 0.6 & 1.0 \\ 0.0 & 0.0 & 0.3 & 0.6 & 0.6 \\ 0.0 & 0.0 & 0.3 & 0.3 & 0.3 \\ 0.0 & 0.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 0.0 & 0.0 \end{array}\right] = (0.0,0.0,0.3,0.6,0.8)$
用最大隶属度法进行决策得风门开度为5。
用加权平均判决法和中位数法进行决策得风门开度为4。

搜索求解策略

搜索求解

分类
- 数据驱动、目的驱动、双向搜索
- 盲目搜索：在不具有对特定问题的任何有关信息的条件下，按固定的步骤（依次或随机调用操作算子）进行的搜索。
- 启发式搜索：考虑特定问题领域可应用的知识，动态地确定调用操作算子的步骤，优先选择较适合的操作算子，尽量减少不必要的搜索，以求尽快地到达结束状态。
状态空间表示法
- 状态：表示系统状态、事实等叙述型知识的一组变量或数组 $Q= [q_1,q_2,\dots,q_n]$
- 操作：表示引起状态变化的过程型知识的一组关系或函数 $F= {f_1,f_2,\dots,f_m}$
- 状态空间：利用状态变量和操作符号，表示系统或问题的有关知识的符号体系，状态空间是一个四元组
  $(A,O,S_0,G) \\ S: 状态集合 \\ O: 操作算子集合\\ S_0: 包含问题的初始状态是S的非空子集\\ G: 若干具体状态或满足某些性质的路径信息描述$
- 求解路径：从 $S_0$ 结点到 $G$ 结点的路径
- 状态空间解：一个有限的操作算子序列

回溯法

回溯法原理：回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。
回溯法步骤
- 用未处理状态表（NPS）使算法能返回（回溯）到其中任一状态。
- 用一张“死胡同”状态表（NSS）来避免算法重新搜索无解的路径。
- 在PS 表中记录当前搜索路径的状态，当满足目的时可以将它作为结果返回。
- 为避免陷入死循环必须对新生成的子状态进行检查，看它是否在该三张表中。

思想：回溯法解决的问题都可以抽象为树形结构，因为回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度，都构成的树的深度。递归就要有终止条件，所以必然是一棵高度有限的树（但是递归通常深度之深难以计算）。
回溯法解决的问题
- 组合问题：N个数里面按一定规则找出k个数的集合
- 切割问题：一个字符串按一定规则有几种切割方式
- 子集问题：一个N个数的集合里有多少符合条件的子集
- 排列问题：N个数按一定规则全排列，有几种排列方式
- 棋盘问题：N皇后，解数独等等
回溯搜索的算法
- PS(path states)表：保存当前搜索路径上的状态。如果找到了目的,PS就是解路径上的状态有序集。
- NPS (new path states)表：新的路径状态表。它包含了等待搜索的状态，其后裔状态还未被搜索到,即未被生成扩展。
- NSS (no solvable states) 表: 不可解状态集，列出了找不到解题路径的状态。如果在搜索中扩展出的状态是它的元素,则可立即将之排除,不必沿该状态继续搜索。

宽度优先搜索（BFS）

宽度优先搜索(breadth-first search，广度优先搜索)：以接近起始节点的程度（深度）为依据，进行逐层扩展的节点搜索方法。

open表（NPS表)：已经生成出来但其子状态未被搜索的状态。
closed表（ PS表和NSS表的合并）：记录了已被生成扩展过的状态。

深度优先搜索（DFS）

深度优先搜索（Depth-first Search): 首先扩展最新产生的节点, 深度相等的节点按生成次序的盲目搜索。

防止搜索过程沿着无益的路径扩展下去，往往给出一个节点扩展的最大深度——深度界限；
与宽度优先搜索算法最根本的不同：将扩展的后继节点放在OPEN表的前端。
深度优先搜索算法的OPEN表后进先出。

题目：01背包

例题

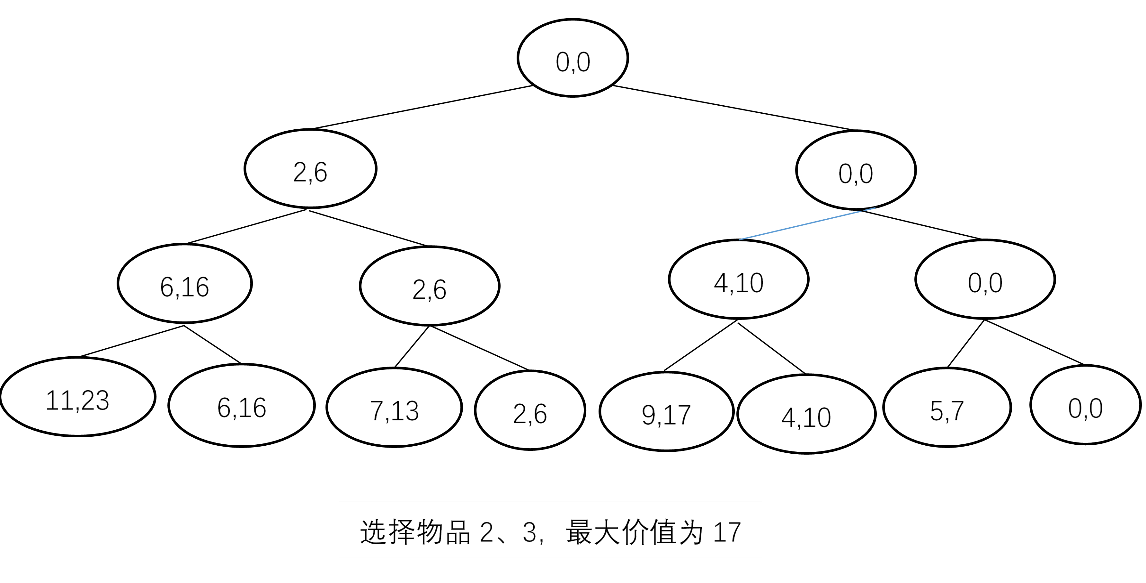
使用回溯法解0/1背包问题
$N=3, C=9, W={2,4,5}, V={6,10,7}$

其解向量x由长度为3的0-1向量组成，并画出其解空间树（从根出发，左1右0），计算其最优值及最优解。

解答

这个问题中每个物品要么装入，要么不装入（向左走加入，向右走不加入），其解空间是一棵子集树 ${x_1,x_2,x_3}, x_i = {0,1}$，有三层，每层代表每个物品的一个决策，树中每一个结点表示背包的一种选择状态，记录当前放入背包的总重量和总价值，每个分枝结点下面由两条边表示对某物品是否放入背包的两种可能的选择。

过程

题目：积木问题

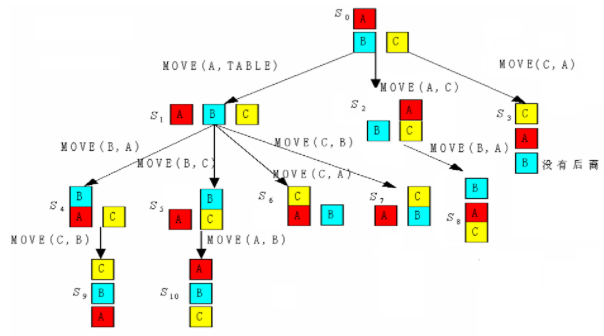
例题

通过搬动积木块，希望从初始状态达到一个目的状态，即三块积木堆叠在一起。

要求

算子MOVE（X，Y）的先决条件：

被搬动积木顶必为空

若Y是积木，Y顶部也必须为空

同状态下操作算子运用次数不得多于1次

过程

Open表：S6， S7 ， S8 ，S9 ， S10

Closed表：S0 ，S1 ，S2，S3 ，S4，S5

扩展节点数：6

生成节点数：10

题目：卒子穿阵

题目

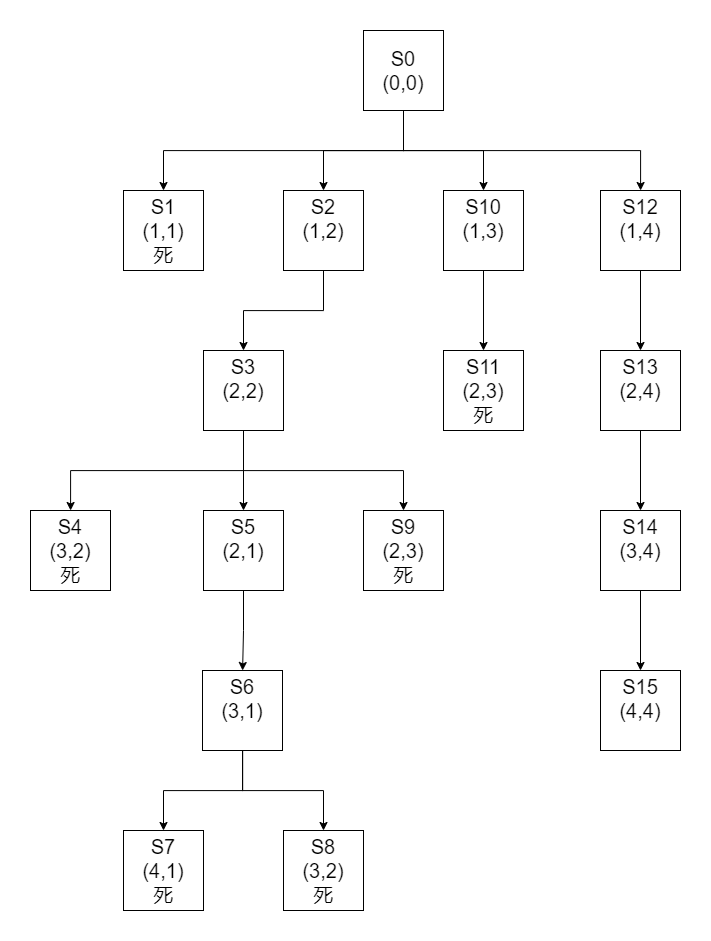
要求一卒子从顶部通过下图所示的阵列到达底部。卒子行进中不可进入到代表敌兵驻守的区域（标注1），并不准后退。假定深度限制值为5。

行\列 1 2 3 4

1 1 0 0 0

2 0 0 1 0

3 0 1 0 0

4 1 0 0 0

步骤

这里做以下规定

从（1，n）出发，为不同出发点，（1，n）的下一个状态只能为（2，n）

（n,m）（n>1）下一个状态优先级依次为： {（n+1,m）,(n,m-1),(n,m+1)}(不能后退)

遇到边缘和敌兵（1）状态为死

最大深度为5

如果求全部路径，直接在（1，n）状态之间平移转换。

如果不限制，maybe：

没有剪枝，大量冗余

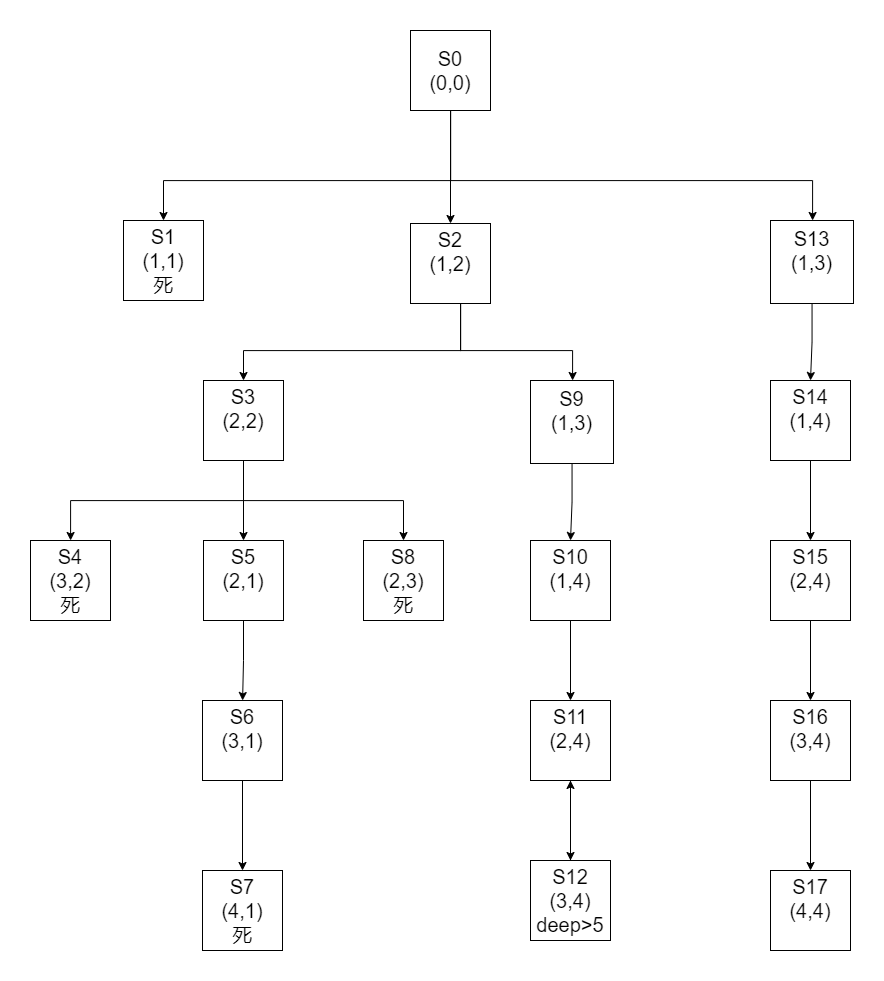
如果加上不可重复进入

maybe：

行\列	1	2	3
1	1	0	0
2	0	0	1
3	0	1	0
4	1	0	0

启发式搜索

运用启发式策略的两种基本情况
- 一个问题由于在问题陈述和数据获取方面固有的模糊性，可能会使它没有一个确定的解。
- 虽然一个问题可能有确定解，但是其状态空间特别大，搜
  索中生成扩展的状态数会随着搜索的深度呈指数级增长。
启发式信息：用来简化搜索过程有关具体问题领域的特性的信息叫做启发信息。
分类
- 运用
  - 陈述性启发信息：用于更准确、更精炼地描述状态
  - 过程性启发信息：用于构造操作算子
  - 控制性启发信息：表示控制策略的知识
- 作用
  - 用于扩展节点的选择，即用于决定应先扩展哪一个节点，以免盲目扩展。
  - 用于生成节点的选择，即用于决定要生成哪些后继节点，以免盲目生成过多无用的节点。
  - 用于删除节点的选择，即用于决定删除哪些无用节点，以免造成进一步的时空浪费。
估价函数：$ f(n)$ 从初始节点经过n节点到达目标节点的路径的最小代价估计值，其一般形式是

$f(n) = g(n)+h(n) \\ g(n)：从初始节点 S0 到节点 n 的实际代价 \\ h(n)：从节点 n 到目标节点 S_g 的最优路径的估计代价，称为启发函数。$

估价函数的任务就是估计待搜索结点的“有希望”程度，并依次给它们排定次序（在open表中）

问答

用状态空间法表示问题时,什么是问题的解?求解过程的本质是什么?什么是最优解？最优解唯一吗？

用状态空间法表示问题时，问题的解就是有向图中从某一节点（初始状态节点）到另一节点（目标状态节点)的路径。求解过程的本质就是对状态空间图的搜索，即在状态空间图上寻找一条从初始状态到目标状态的路径。
在不考虑搜索的代价时，即假设状态空间图中各节点之间的有向边的代价相同时，最优解就是解路径中长度最短的那条路径，在考虑搜索代价时，最优解则是解路径中代价最小的那条路径。因为在状态空间图中，可能存在几条长度或代价相等的最短解路径，所以，最优解可能会不唯一。
回溯算法和DFS(深度优先搜索)到底有什么区别？

回溯是一种思想，核心是不断尝试，不行就推到上一步。深度优先遍历是一种具体算法。
一种说法认为是回溯法=树的深度优先搜索+剪枝函数。但考虑到适用结构，也并不完全对。
回溯算法跟深度优先搜索算法都很经典，它们的区别跟关联都在于它们的数据结构，回溯算法是树结构，深度优先搜索是图结构。树与图的相似点跟不同点导致了回溯算法跟深度优先搜索算法去的存在相以点、也存在不同点。

CUMT课程笔记

#算法 #人工智能

《人工智能控制》笔记

https://junyaohu.github.io/2022/04/18/《人工智能控制》笔记/

作者

胡椒

发布于

2022年4月18日 18:44

更新于

2022年5月21日 14:27

许可协议

ROS学习笔记上一篇

基于滴答清单的时间管理下一篇